谁能想到,一道市级高考数学模拟题,竟能在网上引起轩然大波...
上面这道题目源自刚刚结束的长沙市一模(2026年高三年级模拟考试),因其极高的逻辑密度和对空间想象力的极致要求,在考后引发了数学圈的广泛讨论。
如果你真的认真做了这道题,会发现它不仅仅是一道题目,更是把同学们的数学水平切分成多种境界的“利刃”。
第一境界:初窥门径——有思路,知道拿到这题要画图分类讨论;
第二境界:略有所成——画出了7(或9)种四棱锥的情况,发现这题是道错题;
第三境界:登堂入室——发现其中一种四棱锥5条棱长为1,3条棱长为根号2,不符合条件,所以一共6(或8)种情况;
第四境界:出神入化——思考“镜面对称”是否对应同一种四面体,发现这题不仅选项设置错误,题目也有歧义。进一步思考三维几何体全等的“硬标准”。
我也好奇一下,大家在哪个境界呢?
回归正题,我们先来看看我对这道题的解析,目前处于第三境界——发现这题是一道错题。
附:73Dsi小站提供了非常清晰、直观的6种构造。
进一步,我们探索第四境界——镜面对称(手性对称)的两个四棱锥是否算两种四棱锥?
这就来到了争议爆发点: 在三维空间中,一个手性对称(左手型和右手型)的几何体,到底算一个还是两个?如果算上镜像,答案是8;如果不算镜像(即几何全等),答案是 6。
可惜的是,这个问题在高中阶段没有标准答案。所有困惑的原因,是题目命制的不严谨。
那么当前数学届,是如何“解决”这个问题的呢?他们采用了如下定义:将能够通过平移、旋转、反射变换和彼此重叠两个几何体,定义为全等的。在这个定义下,这题答案毫无疑问,是6个。
然而,数学家的困惑并没有完全解决。一个非常重要的问题被提出:在二维空间中,如果你知道三角形的三条边长,形状就固定了。但在三维空间中,如果你知道一个多面体每个面的形状,以及它们是如何连接的,它的整体形状是唯一的吗?
1813年,数学家柯西(没错,就是那个发明微积分,还有冠名柯西不等式的天才)证明了一个著名的定理:柯西刚性定理。
柯西刚性定理:两个凸多面体,如果它们的面完全相同,且面与面之间的连接关系也相同,那么这两个多面体就是全等的。
这意味着对于凸多面体(没有“坑”的多面体),只要“皮”固定了,形状就死死锁住了。简单来说:如果你把一个凸多面体的每一张“皮”都剪下来,只要这些皮的形状固定了,你重新拼回去的时候,形状是锁死的。你无法通过推拉顶点让它像折叠纸盒一样发生形变。
然而,这个困惑并未结束!如果多面体是凹的,结论就完全失效了。1897年,数学家布里卡尔发现,某些凹八面体即使面完全全等,竟然可以像机械臂一样连续变形!这打破了人们对“形状由边长决定”的直觉认识。有些凹多面体即便所有面的形状和连接方式都一样,你仍然可以像“折纸”一样让它产生形变,得到完全不同的几何体。
配图来源:知乎@斯宾王
然而,布里卡尔的发现带有一个“作弊”嫌疑:他的模型在变形过程中会发生面与面的自相交。直到1977年,康奈利终于构造出了第一个非自相交的柔性多面体(我们都不需要知道这是什么,当科学读物看看就好了)。这个物体像是有生命的细胞,你可以按压它、拉伸它,它的每一条棱长都没有改变,但它的形状却在连续流动。这在当时极大地冲击了人们对几何稳定性的认知:原来,边长并不总是能定义形状。
回到长沙一模的题目,它虽为“错题”,但由于命题角度新颖,题目简洁,仍然成为了人们津津乐道的“顶流题”。这种“顶流”现象的背后,折射出的是教育界对高阶思维与数学本源的深度渴求:我们早已不再满足于在机械的题库中打转,而是渴望在考卷上遇见数学真正的灵魂。
据群友@Claris消息,后续长沙市命题组已对这道题进行“勘误”,调整后的题目就没问题了,但难度早已远超第7题...
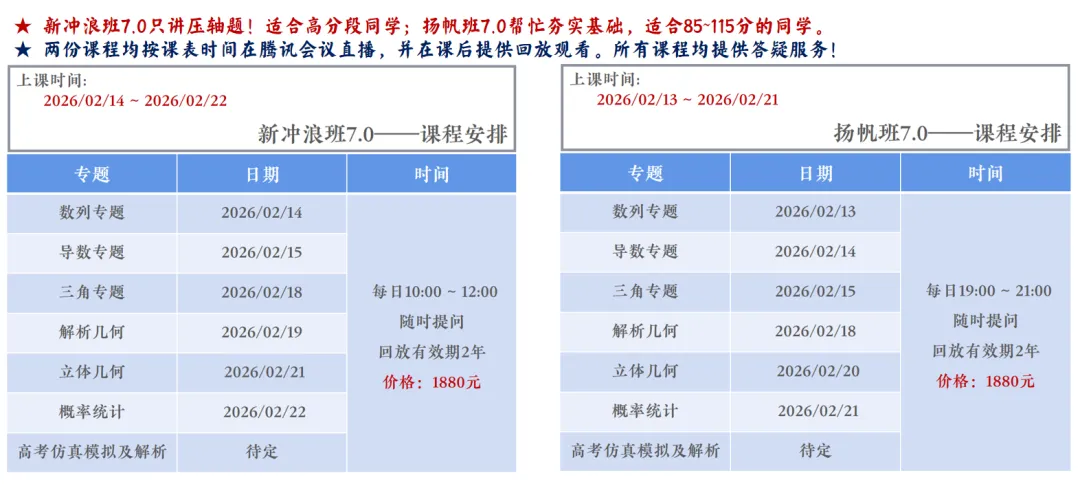
★ 以上是数海漫游寒假课程,报名请联系微信号:shuhaimanyou666。