各位观众朋友们大家好！几天不见甚是想念啊！这两天没有更新主要是因为风姿同学放假回家后正在跟床上的被子交战，奈何被子实在太重压得风姿同学实在是起不来……

After all，今天我们给大家带来的是苏州零模 和 长沙一模。有兴趣的同学可以把原卷找来试试看。特别注意的是长沙一模的第七题还有争议，那个题最好先跳过去。

只需简单转化 | 苏州 T8 单选压轴

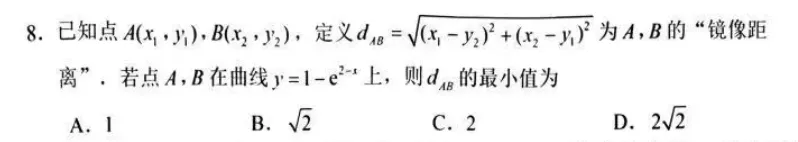
题目里给的“镜像距离”

有一个非常关键的等价变形：

令 （把  关于直线  交换坐标得到的“镜像点”），则

也就是说：镜像距离就是点  到点  的镜像  的普通欧氏距离。

好了这下来 我们就知道了，我们只需要求  和他反函数上的点的最短距离即可。反函数是 。

设最近点分别为

记

两曲线在最近点处，连线  必须同时垂直两条切线方向 ，即

相减得

若  则两曲线相交，但可检验本题这两条曲线不相交（且选项也不含 0），因此取

计算导数：

令公共斜率

则

同时

再代入第一条垂直条件：

左边

右边

于是

可解得唯一正解 。

当 ：

最短距离

烧脑组合 | 长沙 T18 概率组合

哦内盖又是讨厌的组合题呢……

（1）若  且  枚举所有满足条件的 

 等价于  或 

• 若  则  且至少一个包含 1

• 若  同理

所以共有 6 组

（2）求 

对每个元素  定义指示变量。

则

从而

在等可能随机子集中 任一元素被选入某个子集的概率为  且两次选择独立 因此

所以

从而

（3）若  在  处取得最大值 建立  与  的函数关系

对固定元素  事件  发生概率为  且不同元素之间相互独立 因此

二项分布众数性质

• 若  不是整数 则唯一众数为 
• 若  是整数 则有两个并列众数  与 

这里  且

因此